2006, Vol.13, pp.207-228

In the paper, the known possibility to consider the (vacuum) Maxwell equations in a curved space-time as Maxwell equations in flat space-time (Mandel'stam L.I., Tamm I.E. [1,2]) but taken in an effective media the properties of which are determined by metrical structure of the initial curved model is studied. Metrical structure of the curved space-time generates the "material equations" for electromagnetic fields:

the form of four symmetrical "matherial" tensors is found explicitly for general case of an arbitrary Riemannian space-time geometry :

Several, the most simple examples are specified in detail: it is given geometrical modeling of the anisotropic media (magnetic crystals)

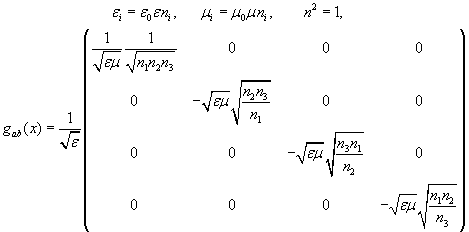
and the geometrical modeling of a uniform media in moving reference frame in the background of Minkowsky electrodynmamics -- the latter is realized trough the use of a non-diagonal metrical tensor determined by 4-vector velocity of the moving uniform media The main peculiarity of the geometrical generating for effective electromagnetic medias characteristics consists in the following: four tensors are not independent and obey some additional constraints between them.
Key words: Maxwell equations, curved space-time

Full text:  Acrobat PDF  (205KB)